Zero-Knowledge Proofs: what are zk-STARKs and how do they work? (zk-Stark V2)
What is Proof-of-Reserve and Zero Knowledge Proof?
Proof-of-Reserve (PoR)
This is a process for cryptocurrency exchanges to show they have enough assets to cover all customer balances. This builds trust by proving the exchange is not hiding any liabilities. The simplest way to show this is by publishing both the exchange's asset amounts and a list of user balances so everyone can confirm:
The total user asset holdings that we claim to hold is the sum of every user's total asset balance
Every user's total balance is more than zero, and their assets are accounted for, covering their liabilities and ensuring that each user has positive net equity
The total value that the exchange claims accounts for every single user, so every user should be able to verify the inclusion of their net value in the total value
However, revealing these balances can compromise user privacy. To solve this, we use a method called Zero Knowledge Proof (ZKP) to safeguard user's privacy.
Zero Knowledge Proof (ZKP)
It's a security technique that allows cryptocurrency exchange to prove a statement is true without revealing any additional information.
In our case, we want to prove that we have enough funds without sharing specific user details. Most ZKPs fall under two categories:
zk-SNARK
zk-STARK
We use zk-STARK because it's more secure and has a minimum security assumption. In this article, we'll explain how we use zk-STARK to protect user privacy while proving our solvency.Before we continue, it's helpful to understand some basic ZKP terms, like Circuit, Merkle Tree, and Commitments.
For beginners, there are many resources available to help you get started. For advanced users, you may refer to the MOOC Course and the academic monograph.
How does zk-STARK work?
We create a Merkle tree using the hash of each user's account as the leaves. Each account shows balances in USD for various tokens (e.g., BTC, ETH). To handle these balances, we separate its balances into non-negative equities and debts for each token. This way, we only work with positive numbers, making it easier to handle calculations and avoid errors.
For example:
If a user's BTC token balance is A, its BTC equity is A and BTC debt is 0
If a user's ETH token balance is -B, its corresponding equity is 0 and the debt is B
Next, we build a Merkle tree with these account values as leaves. The root of the tree acts as a single value representing all user balances. Each user can prove their account is part of this tree by using a Merkle Path that shows how their account connects to the root.
We also publish the total equity and debt summed across all tokens and users. Then, we create a Zero Knowledge Proof (ZKP) to show two things:
Sum Proof: the equity and debt values in the Merkle tree add up correctly
Non-negative Proof: each user's total equity is greater than their total debt
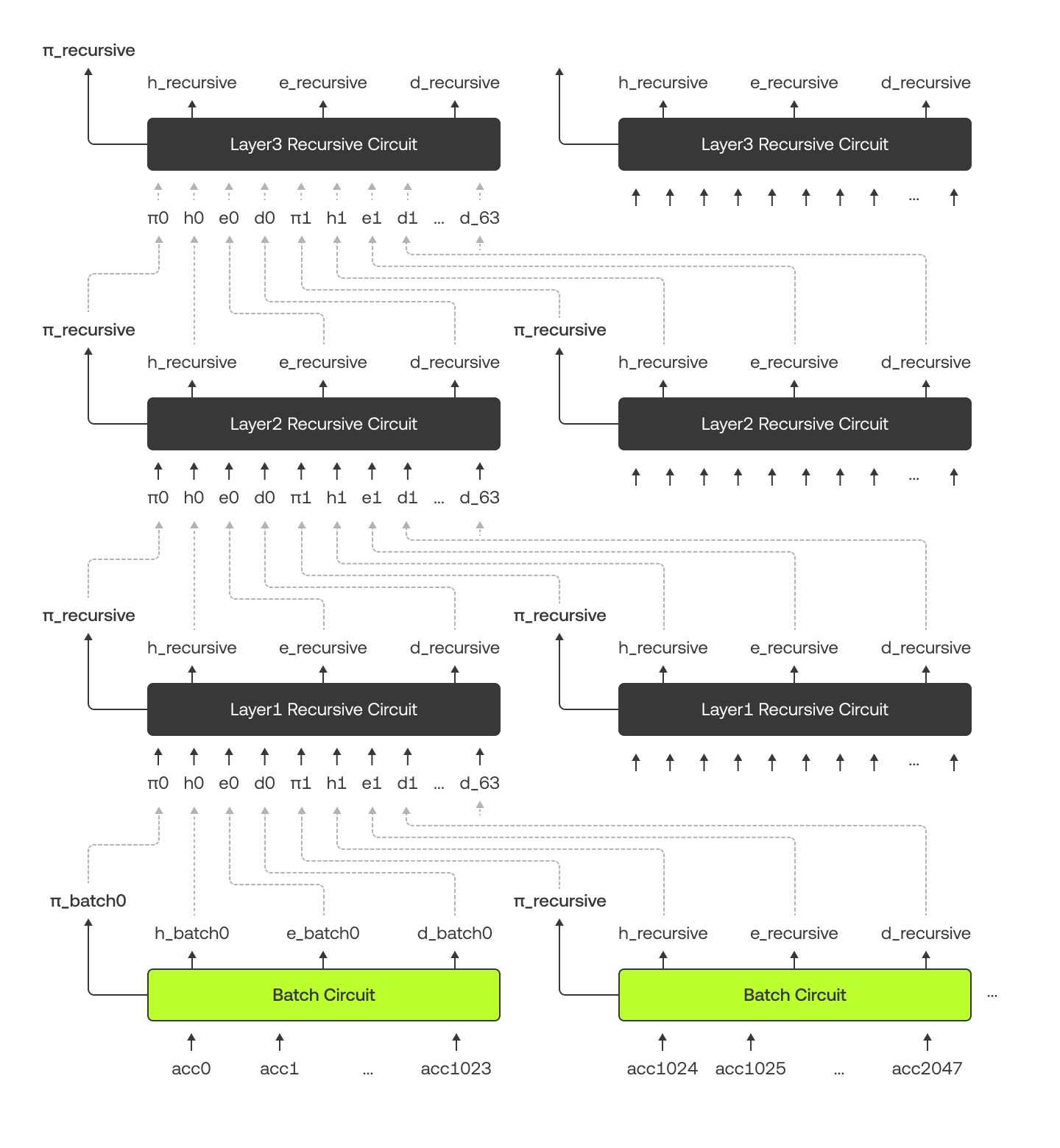
When we try to verify the Merkle tree for a large number of accounts, it becomes too much to handle in one go. To overcome this challenge, we break the accounts into smaller groups called batches. Each batch is processed separately using batch circuits, which checks the bottom portion of the Merkle tree.
Batching not only makes it manageable but also allows us to run these checks at the same time (parallel processing). Once we have the results from each batch, we use another layer of circuits, called recursive circuits, to combine and verify all the batches together, until we've proven the entire Merkle tree.
What is Batch Circuit?
The batch circuit takes in 1024 accounts (acc0, acc1,..., acc1023) as inputs and generates 3 main outputs: a hash (hbatch), a total equity value (ebatch) , and a total debt value (dbatch). It checks that:
Each account's total USD-denominated equity is greater than its total debt
ebatch is the sum of all the USD-denominated equity values across these accounts
dbatch is the sum of all the USD-denominated debt values across these accounts
hbatch is the root of the Merkle tree created using the accounts' hashes
There is no overflow during the summation for ebatch and dbatch
What is Recursive Circuit?
The recursive circuit takes 64 different proofs (π0, ..., π63), hashes (h0, ..., h63), equities (e0, ..., e63), and debts (d0, ..., d63) from the lower-layer circuits as inputs. It combines these inputs and produces 3 outputs: a new hash (hrecursive), total equity (erecursive), and total debt (drecursive). It checks that:
Each of the 64 proofs is valid
Each proof π0, ..., π63 from the lower-layer circuit is valid
erecursive is the sum of e0, ..., e63
drecursive is the sum of d0, ..., d63
hrecursive is the hash of the concatenation of h0, ..., h63, i.e.
hrecursive = Hash (h0 || h1 || ... || h63)
There is no overflow during the summation for erecursive and drecursive
What is the relationship between batch circuits and recursive circuits?
The diagram below illustrates how the batch circuit and recursive circuits connect and pass data between each other. Keep in mind that in the diagram, we duplicate the circuits for illustration purposes, but in our implementation, we only use one circuit for each layer.
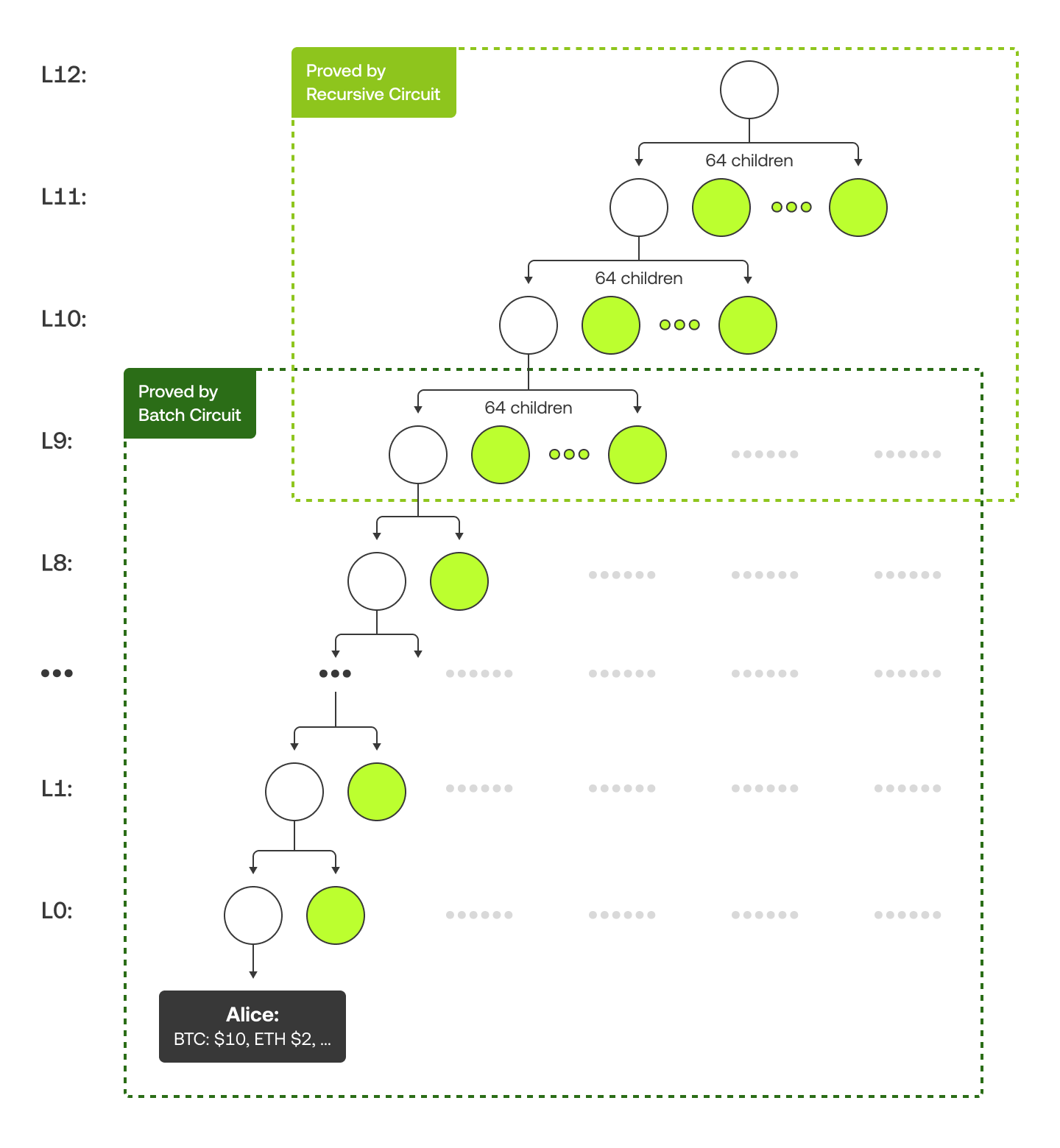
Our Merkle tree is structured a bit differently. At the bottom 10 levels, each parent node has 2 children, while in the upper levels, each parent has 64 children. This is because the batch circuits handle the bottom part, and the recursive circuits manage the top part. The diagram below uses an example with "Alice" to show the Merkle tree and her Merkle proof (colored in green).
For more technical details, such as how we adjust account numbers to fit the batch size or choose the right hash algorithm, check out this page.
Advances in zk-PoR Version 2
Our zk-PoR Version 2 has made several advances from the previous version:
Greater efficiency: It is now 50 times faster than the previous version. It takes 3 hours on a single 10-core machine, compared to previous version's 36 hours using nine 64-core machines. This speedup is due to the usage of the Plonky2 framework, which compiles Rust-coded circuits into efficient machine language instead of using slower Python scripts. We also enhanced Plonky2 to run some computations on GPUs, reducing the time by an extra 30%.
Better auditability: With Version 2, we use a high-level framework that handles complex cryptographic details for us. This makes our code clearer, more readable, and less prone to errors.
Concise proof: The V2 proof size (~500KB) is only 0.05% of V1 (~1.2GB). Thanks to the recursive method, the proofs can be repeatedly aggregated and condensed into a single proof.
How do I perform self-verification of Proof of Reserves (PoR)?
Here's how you can check if your asset balance is included as a zk-STARK Merkle leaf:
Log in to your OKX account, go to Assets and select PoR reports
Select Details to view your audit data
Get the data you need for manual verification by selecting Copy data
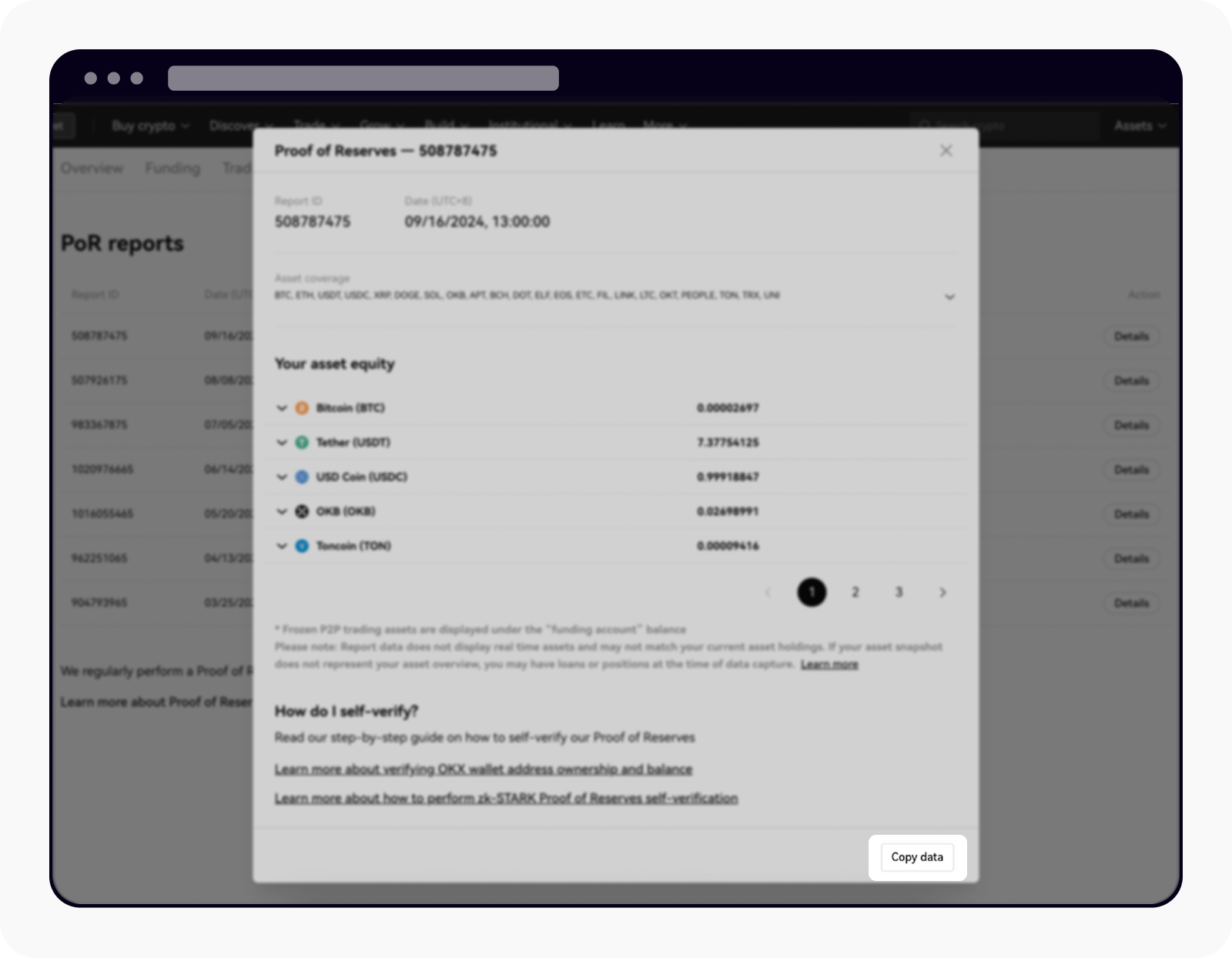
After selecting Copy data, open the text editor (e.g. using notebook) then paste and save the JSON string as a file. The file must end with the name "_inclusion_proof.json." The JSON string contains your account balance and a snapshot of the Merkle path, then saves the file in a new folder.
Open a text editor (e.g., Notebook), then paste and save the JSON string as a file. The file name must end with "_inclusion_proof.json." Save the file in a new folder.
The JSON string contains your account balance and a snapshot of the Merkle path.
The JSON text is shown below:
{"sum_tree_siblings":["9ffb169fecf075e203edca2af65e4c69fa4331d13ac75ccae4cd5b990c91b675","7149661a789763cb61293ebf5d8bdd5570e79ee203738f87a444c79642b89a79","788aac9e392fa62bc3f79c98c7afd7bb41ee7d5bd496876cd0580080f19e002f","e828a44d345e6799e232aabc57cb2b92986ee1c52b65344d83e79d84b4b571b7","6c0675de9cd6b2be1abd6a98260e7ea776492c4aa9aadf31086f23452cb7c48d","2dfe3aadb5ac00ee0b1110ee8c313afdee85d9f9c62904d6ee79c8f02354d80a","5068ae26192587432892a6de8b54ea25a8aafd1c010ab5e67b55b2c30c6257fa","a1bb026ec9f3d8a1fa1b6f498c40ed8b117a57e1af9816d08d9135ab4fe43a60","119dfcd214191405b7f7f7c7091b89196c0cae818bfcd8252a48f20d9cf3c378","4d9403482ca177c669df34a60bb2afab7a18097012d0b70703c8e59258cdfee6"],"recursive_tree_siblings":[{"right_hashes":["e041eaa366259f873e9e1477aac77362f4b1b460c2d5e1c14907fa9288d66cff","b45a8c503e649ff39543a918996b06fc65f4df9b61d071b22f7342f94862c9be","e00ec1225dfe6b7e950f6b9b8e9d1121bf17eb60c444fd7191b861a2ddddad23","c02c12beb73c03f996508cdce7bef927f0aa8b77ebd899f6a75df83de9d4022e","d36b95f14c5fd5bfaf1347e3177340e2fc9475a77b852321b80527132e7d539c","c0b9770178e70a7bba4ac8aeaadab2bcb2ae7f90d0f678bd463f2c42ff4f4a7b","fab5e7c6f7f8bc6d51f515c5db235cc1ebe987adee8c19c9bc7313e9e266d72c","b3884fb88fc95949c78ca8867cfa9e8a3c4c59fa1a48d8371f7fbfbebda0acfd","0c6da9bdbd40065f92ddaa45297670f2f0bffedb74020c5d5752e70d8b507b77","left_hashes":["1101beee3c6a36a168ceee9d43fcf6cb6de7e5c87ed4d22cd0308c9870d17839","d40a8e9eb4c873996ec515600def480eaa9378ca8481a7bcdf5f77725dbec4ae","63b12566ba8473f502386e92d500664cb63683dca6c26593378dcc9715257b77","166440a8ccbfbc1ce6ec5efaf8bc0b25e1bf692fa972e2729e45ce709d1d35a3","724451ad1d937fc47de5ede930d159dce78093d5e6a1f2e698452f8a29b4de3a","081a88f12d4e23173a1bf5038d4a9413cc92dd421c92261065de06492b5010ec","a76dbb1d4c393539b9546f4460d50ebc7582748d7de63c62c463b793c55bac7c","91e6c21de3f4060e1bd864131a570af42de31bbcd84a5afcbbc8fedcbf806002","fad08eca5bfdc5f37d39eabb44c2216afc6498afcb6b913d72586eaaf132a572","d39b06fe28387ba8045e2b2f95e90613916beef4f79df7961514e6e4cbfd07fa","81d07e300a116a0e4fcb56c39715c5fd5921abe8d10329b07c3f33d417b70ca8","7b72a7e62a45c9958a8a55eec2ba47352f2af701bacba098668589f6a3ce0423","8766bc64c38c2bb4188d89de0e732bca103daaed0c779cba9a8b191e24b51c9c","fa57ae4409e46c605f3cbfd01dfd9ccebc86cbd765cdc067206cb9367832442f"]}, ...... "index":9583119,"account":{"id":"50f5f08cc5036e15a541c64ac4ac6d2d9aa8ddab1ec32ed58b10e6ed3edfad59","debt":["0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"],"equity":["8412384","9386185","45265193","0","0","8751","3824171","2716990","0","313671","28319","0","0","0","41261","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","142353","0","0","0","0","0","4435","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","662","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","993","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","25132","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","305","0","0","0","0","0","0","0","0","6141","0","0","0","0","0","0","0","0","0","0","0","5511","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"]}}
Download the OKX open-source verification tool: zk-STARKValidator
Save the OKX open-source verification tool, zk-STARKValidator, and the JSON string file together in the new folder created in Step 5. In our case, we placed the tool and the data file in the Downloads folder, named "proof-of-reserves," as shown below:

Open the zk-STARKValidator; it'll automatically run the JSON file you saved in the folder
Check the result:
If the verification passes, the result Inclusion constraint validation passed will be shown:

If the verification fails, the result Inclusion constraint validation failed will be shown:

How do I verify the zk-STARK total balance and non-negative constraint?
Here's how you can verify that the assets we claim to hold are true and that no user holds negative net equity:
Go to our Proof of Reserve page and select Liability report
Download the zk-STARK file and save it in a new folder
Unzip the file to extract a "sum_proof_data.json" file

Download the OKX open-source verification tool: zk-STARKValidator
Save the OKX open-source verification tool, zk-STARKValidator, and the "sum_proof_data.json" file together in the new folder created in Step 2. In our case, we placed the tool and the data file in the Downloads folder, named "proof-of-reserves," as shown below:

Open the zk-STARKValidator; it will automatically run the sum proof data file you saved in the folder
Check the result
If the verification passes, the result Total sum and non-negative constraint validation passed will be shown:

If the verification fails, the result Total sum and non-negative constraint validation failed will be shown:

To explore more technical details, our Proof of Reserves system is open-source and available for review and use on github.






