Explanation for Greeks Delta and Gamma
Options Greeks are a measure of the risks involved in taking an options position. Delta and gamma are two options greeks related to underlying price.
In traditional options trading, delta and gamma, as known as BS delta and BS gamma, are derived from the Black-Scholes or Black options pricing model. BS delta measures the rate of change of the option price relative to the change of underlying price. BS gamma measures the rate of change of BS delta relative to the change of underlying price.
For the OKX BTCUSD options contract, the calculation of delta and gamma is different from the traditional way. They are derivatives of the Black options pricing model with a price adjustment, and we call them PA delta and PA gamma.
The relationship between BS delta and PA delta is as below:
PA Delta = BS Delta - Options Mark Price (In BTC)
PA delta measures the rate of change of the option price relative to the percentage change of the underlying price. And PA gamma measures the rate of change of PA delta relative to the percentage change of the underlying price.
The below example further illustrates the differences between PA delta and BS delta:
Assume the BTCUSD index price is 7,000 USD, the BS delta of a BTC options contract is 0.6, and PA delta is 0.45. When BTCUSD rises 105 USD (1.5% up),
Based on the BS delta calculation, the option price will increase by 0.6 * 105 = 63 USD
Based on the PA delta calculation, the option price will increase by 0.45 * 1.5% = 0.00675 BTC
That is, when using BS delta to estimate the option price change, we take the underlying price change in USD (USD105); when using PA delta, we take the percentage change of the underlying price (1.5%).
Using the same example, we can tell the difference between PA gamma and BS gamma:
Assume the BTCUSD index price is 7,000 USD, the BS gamma of a BTC options contract is 0.0004, and PA gamma is 2.9. When BTCUSD rises 105 USD (1.5% up),
Based on the BS gamma calculation, the BS delta will increase by 0.004* 105 = 0.042 USD
Based on the PA gamma calculation, the PA delta will increase by 2.9 * 1.5% = 0.0435 BTC
That is, when using BS gamma to estimate the BS delta change, we take the underlying price change in USD (105 USD); when using PA gamma to determine the PA delta change, we take the percentage change of the underlying price (1.5%).
1. Reason for using PA delta in OKX
The reason why OKX does not adopt BS delta and gamma, but instead, a different approach to calculate delta and gamma is that the margin and the settlement currency of the OKX BTCUSD options contract is BTC but not USD.
When a trader wants to assess the risk of an option and calculate the hedging positions (such as hedging the delta risk of options with futures contracts), he will get a wrong hedge ratio by using BS delta and BS gamma. Below is an example to demonstrate the hedging efficiency.
Assume the current BTCUSD index is 7,000 USD. A user longs 10 put options contract BTCUSD-200327-20000-P (A put option with an exercise price of 20,000 USD and expiration date on March 27, 2020), and wants to hold some futures contract with the same expiration date to hedge the delta risk fully.
The following two tables show the information of the options contract and futures contract.
|
BTCUSD-200327-20000-P |
||
|
Mark Price |
PA delta |
BS delta |
|
1.8571 BTC |
-2.85702309 |
-0.99993983 |
|
Quarterly BTCUSD0327 |
|
|
Mark Price |
delta |
|
7,000 |
0.01428571(=100/7,000) |
The number of futures contracts calculated by using PA delta for hedging is:

The number of futures contracts calculated by using BS delta for hedging is:

A positive number indicates a buy, and a negative number indicates a sell. There are two delta hedging portfolios formed:
|
|
BTCUSD-200327-20000-P |
Quarterly BTCUSD0327 |
|
PA portfolio |
10 contracts |
200 contracts |
|
BS portfolio |
10 contracts |
70 contracts |
Holding other factors constant, when the spot index changes, the profit and loss (PnL) status of the two portfolios will be changed as follows:
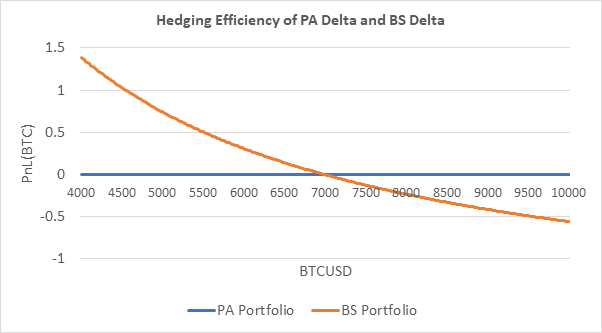
From the above graph, we can see that as the spot index changes, the PnL of the PA portfolio remains as 0, while the PnL of the BS portfolio deviates significantly from 0. Therefore, using BS delta to calculate the hedge position leads to a wrong result. On the other hand, PA delta provides a correct hedge position. The root cause is that BS delta and BS gamma cannot be truly reflected the actual option risk in BTC margined/settled option contracts. There is where PA delta and PA gamma come into play.
Note: The above examples are calculations and judgments on the assumption that only the underlying index changes and other factors remain unchanged. In the actual scenario, the profit and loss of the portfolio will be affected by a variety of factors, such as changes in volatility.
2. The range of PA delta value
BS delta of a call option has a range between 0 and 1, while the BS delta of a put option has a range between -1 and 0.
PA delta has a different range instead. We can get the PA deltas of a put option and call option with the formula below:
PA Delta = BS Delta - Options Mark Price (in BTC)
Based on the formula, we can get the range of a PA delta with BS delta and the option mark price.
[PA delta of a call option ranges from 0 - 1]
When the underlying price increases, the price of a call option increases accordingly. According to the definition of PA delta, the value of PA delta must be greater than 0. And from the equation “PA delta = BS delta – option mark price”, we know that the upper limit of PA delta will not exceed the upper limit of BS delta, 1, as the option mark price is always positive.
[The PA delta of a put option ranges from negative infinity to 0]
When the underlying price increases, the price of a put option decreases accordingly. From the definition of PA delta, we know that PA delta must be smaller than zero. When the underlying price is close to 0, the intrinsic value of the put option (in BTC) is infinite, so there is no upper limit for the option mark price, and the upper limit for BS delta is 0. From the equation “PA delta = BS delta – option mark price”, we know that the PA delta of a put option can be less than -1, and in extreme cases, it can reach negative infinity.
Note: Negative infinity refers to a very small negative number, smaller than any negative number.
3. The Positive and negative value of PA gamma
Gamma measures the rate at which delta changes with the underlying price. If the underlying price increases, the delta value also increases, the gamma will be a positive value; if the underlying price increases but the delta value decreases, the gamma value will be negative. To put simply, the value of the gamma is related to the slope of the delta curve. The curves of the two types of delta are shown as below:
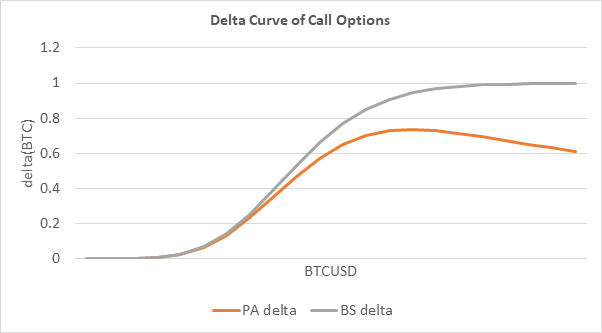
Holding other variables constant, when the underlying price increases, the PA gamma of a call option first increases and then decreases; for BS delta, it increases as the underlying price increases. Thus, the BS gamma of a call option is always positive.
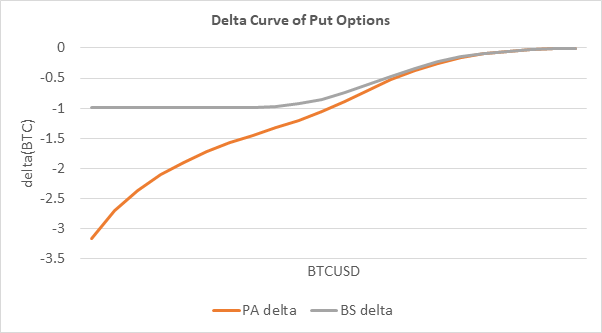
Holding other variables constant, when the underlying price increases, the PA gamma and the BS delta of a put option increase. Therefore, the PA gamma and the BS gamma of a put option will be positive.