Dovezi de cunoștințe zero: ce sunt zk-STARKs și cum funcționează? (zk-Stark V2)
Ce este dovada rezervelor și dovezile de cunoștințe zero?
Dovada rezervelor (PoR)
Acesta este un proces pentru bursele de criptomonede pentru a arăta că au suficiente active pentru a acoperi toate soldurile clienților. Acest aspect construiește încredere prin dovedirea faptului că bursa nu ascunde nicio datorie. Cea mai simplă modalitate de a arăta acest lucru este prin publicarea atât a sumelor de active ale bursei, cât și a unei liste cu soldurile utilizatorilor, astfel încât toată lumea să poată confirma:
Totalul activelor deținute de utilizatori pe care OKX susține că le deține este suma soldului total de active al fiecărui utilizator.
Soldul total al fiecărui utilizator este mai mare decât zero, iar activele lor sunt contabilizate, acoperind pasivele lor și asigurându-se că fiecare utilizator are un capital net pozitiv.
Valoarea totală pe care bursa o revendică reprezintă fiecare utilizator în parte, așa că fiecare utilizator ar trebui să fie capabil să verifice includerea valorii lor nete în valoarea totală.
Cu toate acestea, dezvăluirea acestor solduri poate compromite confidențialitatea utilizatorului. Pentru a rezolva acest lucru, folosim o metodă numită Dovezi de cunoștințe zero (ZKP: zero knowledge proof) pentru a proteja intimitatea utilizatorului.
Dovezi de cunoștințe zero (ZKP)
Este o tehnică de securitate care permite bursei de criptomonede să dovedească că o afirmație este adevărată fără a dezvălui informații suplimentare.
În cazul nostru, dorim să demonstrăm că avem suficiente fonduri fără a împărtăși detalii specifice ale utilizatorului. Cele mai multe ZKP-uri se încadrează în două categorii:
zk-SNARK
zk-STARK
Folosim zk-STARK deoarece este mai sigur și prezintă o presupunere minimă de securitate. În acest articol, vom explica cum folosim zk-STARK pentru a proteja confidențialitatea utilizatorilor în timp ce dovedim solvabilitatea noastră.Înainte de a continua, este util să înțelegem câțiva termeni de bază ZKP, cum ar fi Circuit, Arbore Merkle si Angajamente.
Pentru începători, există multe resurse disponibile ca punct de pornire. Pentru utilizatorii avansați, puteți consulta Cursul MOOC și monografia academică.
Cum funcționează zk-STARK?
Creăm un arbore Merkle folosind valoarea haș a contului fiecărui utilizator sub formă de frunze. Fiecare cont arată solduri în USD pentru diferite tokenuri (deexemplu, BTC, ETH). Pentru a gestiona aceste solduri, le separăm în capitaluri non-negative și datorii pentru fiecare token. În acest fel, lucrăm doar cu numere pozitive, facilitând astfel gestionarea calculelor și evitarea erorilor.
De exemplu:
Dacă soldul tokenului BTC al unui utilizator este A, capitalul său BTC este A, iar datoria BTC este 0.
Dacă soldul tokenului ETH al unui utilizator este -B, capitalul său corespunzător este 0, iar datoria este B.
Apoi, construim un arbore Merkle cu aceste valori de cont sub formă de frunze. Rădăcina arborelui acționează ca o valoare unică care reprezintă toate soldurile utilizatorilor. Fiecare utilizator poate dovedi că contul său face parte din acest arbore folosind o Cale Merkle care arată cum contul său se conectează la rădăcină.
De asemenea, publicăm capitalul total și datoria sumate pentru toate tokenurile și utilizatorii. Apoi, creăm o dovadă de cunoștințe zero (ZKP) pentru a indica două lucruri:
Dovada sumei: valorile de capital și datorie din arborele Merkle se adună corect
Dovada non-negativă: capitalul total al fiecărui utilizator este mai mare decât datoria lor totală
Când încercăm să verificăm arborele Merkle pentru un număr mare de conturi, devine prea mult de gestionat dintr-o dată. Pentru a depăși această provocare, împărțim conturile în grupuri mai mici numite loturi. Fiecare lot este procesat separat folosind circuite de lot, care verifică porțiunea de jos a arborelui Merkle.
Împărțirea pe loturi nu doar că face procesul gestionabil, dar ne permite și să rulăm aceste verificări în același timp (procesare paralelă). Odată ce avem rezultatele din fiecare lot, folosim un alt strat de circuite, numit circuite recursive, pentru a combina și verifica toate loturile împreună, până când am dovedit întregul arbore Merkle.
Ce este circuitul de lot?
Circuitul de lot ia 1.024 de conturi (acc0, acc1,..., acc1023) ca intrări și generează 3 ieșiri principale: o valoare haș (hbatch), o valoare totală a capitalului (ebatch) și o valoare totală a datoriei (dbatch). Acesta verifică faptul că:
Totalul capitalului exprimat în USD al fiecărui cont este mai mare decât datoria sa totală
ebatch este suma tuturor valorilor de capital exprimate în USD din aceste conturi
dbatch este suma tuturor valorilor datoriilor exprimate în USD din aceste conturi
hbatch este rădăcina arborelui Merkle creat folosind valorile haș ale conturilor
Nu există depășire în timpul adunării pentru ebatch și dbatch
Ce este circuitul recursiv?
Circuitul recursiv ia 64 de dovezi diferite (π0, ..., π63), valori haș (h0, ..., h63), capitaluri (e0, ..., e63) și datorii (d0, ..., d63) din circuitele de nivel inferior ca intrări. Combină aceste intrări și produce 3 ieșiri: o nouă valoare haș (hrecursive), capital total (erecursive) și datorie totală (drecursive). Acesta verifică faptul că:
Fiecare dintre cele 64 de dovezi este valabilă
Fiecare dovadă π0, ..., π63 din circuitul de nivel inferior este validă
erecursive este suma lui e0, ..., e63
drecursive este suma lui d0, ..., d63
hrecursive este valoare haș a concatenării lui h0, ..., h63, i.e.
hrecursive = haș (h0 || h1 || ... || h63)
Nu există depășiri în timpul adunării pentru erecursive și drecursive
Care este relația dintre circuitele de lot și circuitele recursive?
Diagrama de mai jos ilustrează modul în care circuitul de lot și circuitele recursive se conectează și transmit date între ele. Rețineți că în diagramă, duplicăm circuitele în scopuri de ilustrare, dar în implementarea noastră, folosim doar un circuit pentru fiecare strat.
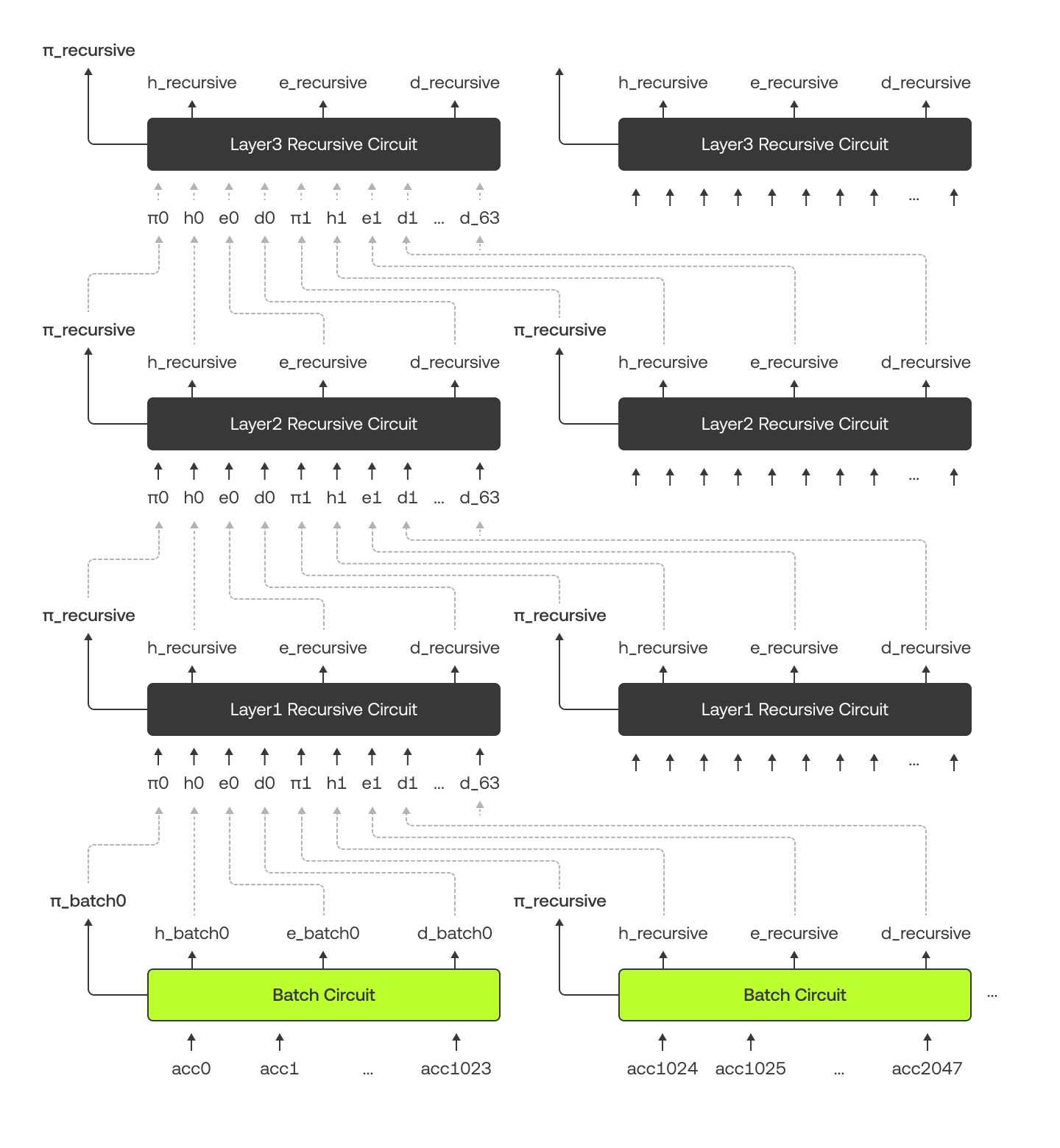
Arborele Merkle este structurat puțin diferit. La cele 10 niveluri de jos, fiecare nod părinte are 2 copii, în timp ce în nivelurile superioare, fiecare părinte are 64 de copii. Acest lucru se datorează faptului că circuitele de lot gestionează partea de jos, iar circuitele recursive gestionează partea de sus. Diagrama de mai jos folosește un exemplu cu „Alice” pentru a arăta arborele Merkle și dovada ei Merkle (colorată în verde).
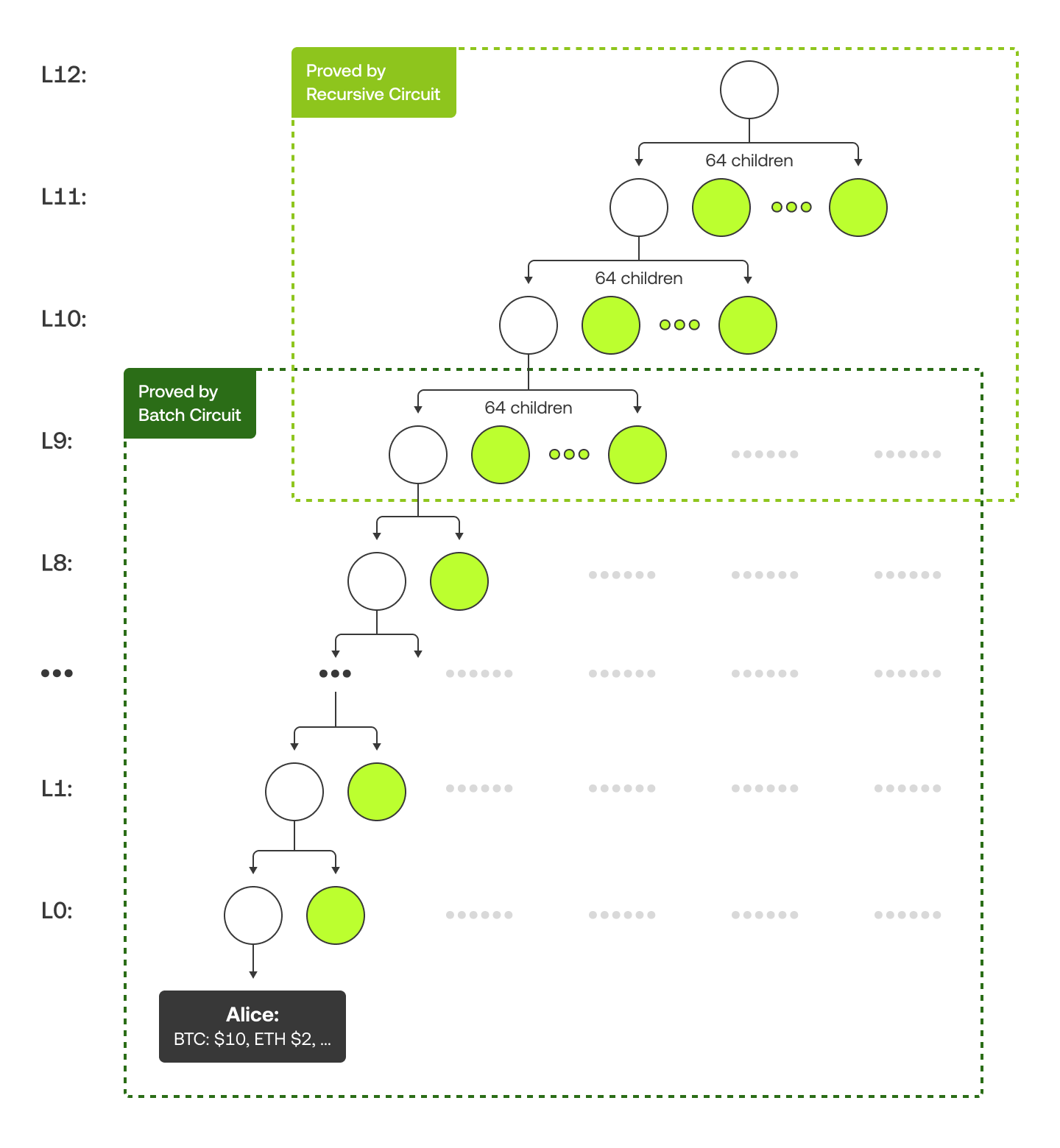
Pentru mai multe detalii tehnice, cum ar fi modul în care ajustăm numerele de cont pentru a coincide cu dimensiunea lotului sau alegerea algoritmului de haș potrivit, consultați această pagină.
Progrese în versiunea 2 a zk-PoR
Versiunea 2 a tehnologiei noastre zk-PoR a beneficiat de mai multe progrese față de versiunea anterioară:
Eficiență mai mare: acum este de 50 de ori mai rapid decât versiunea anterioară. Durata este de 3 ore pe o singură mașină cu 10 nuclee, comparativ cu cele 36 de ore ale versiunii anterioare folosind nouă mașini cu 64 de nuclee. Această accelerare se datorează utilizării cadrului de lucru Plonky2, care compilează circuite codificate în Rust în limbaj de mașină eficient în loc să folosească scripturi Python mai lente. Am îmbunătățit, de asemenea, Plonky2 pentru a efectua unele calcule pe GPU-uri, reducând timpul cu încă 30%.
Auditabilitate mai bună: cu versiunea 2, folosim un cadru de lucru de nivel înalt care gestionează detaliile criptografice complexe pentru noi. Acest lucru face ca codul nostru să fie mai clar, mai ușor de citit și mai puțin predispus la erori.
Dovadă concisă: dimensiunea dovezii V2 (~500 KB) este doar 0,05% din V1 (~1.2 GB). Datorită metodei recursive, dovezile pot fi agregate și condensate repetat într-o singură dovadă.
Cum efectuez autoverificarea dovezii rezervelor (PoR)?
Iată cum puteți verifica dacă soldul activelor pe care le dețineți este inclus ca o frunză Merkle zk-STARK:
Conectați-vă în contul OKX, accesați Active și selectați Rapoarte PoR
Selectați Detalii pentru a vă accesa datele de audit
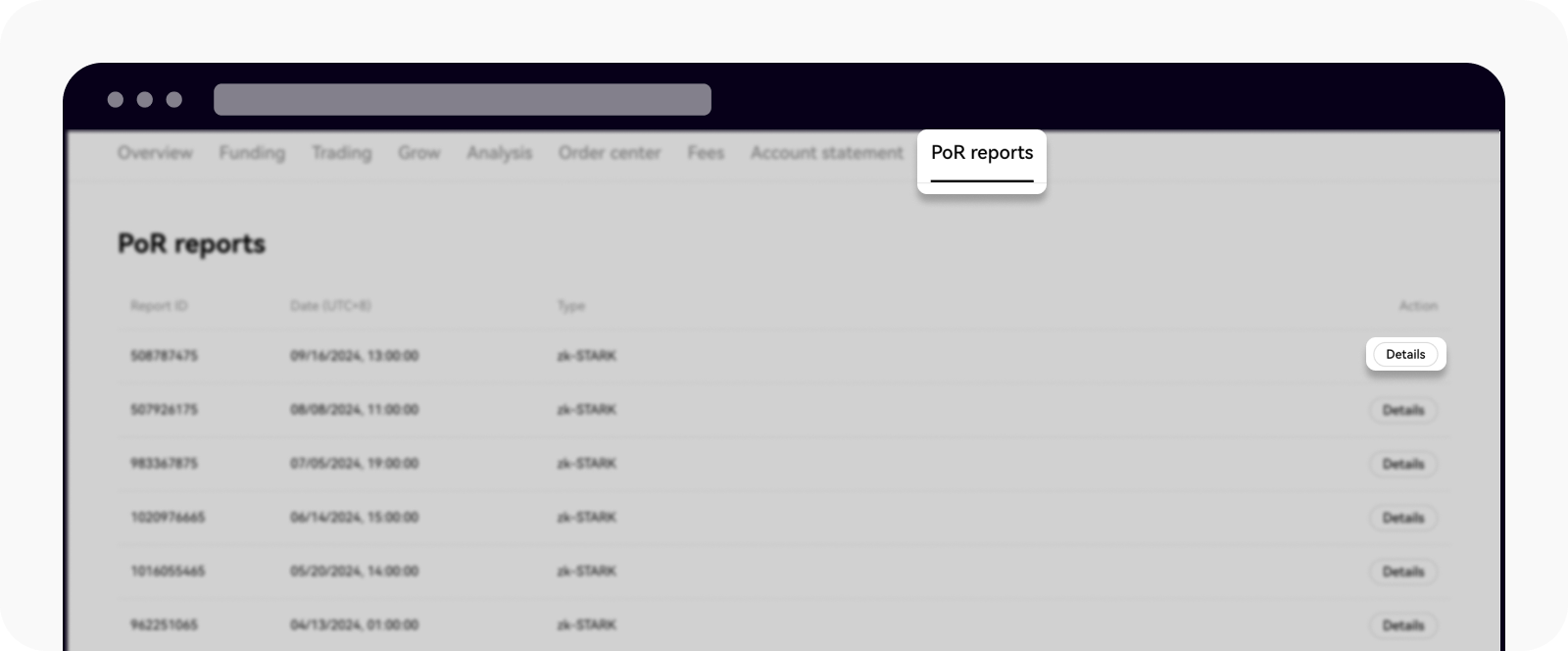
Obțineți datele de care aveți nevoie pentru verificarea manuală selectând Copiere date
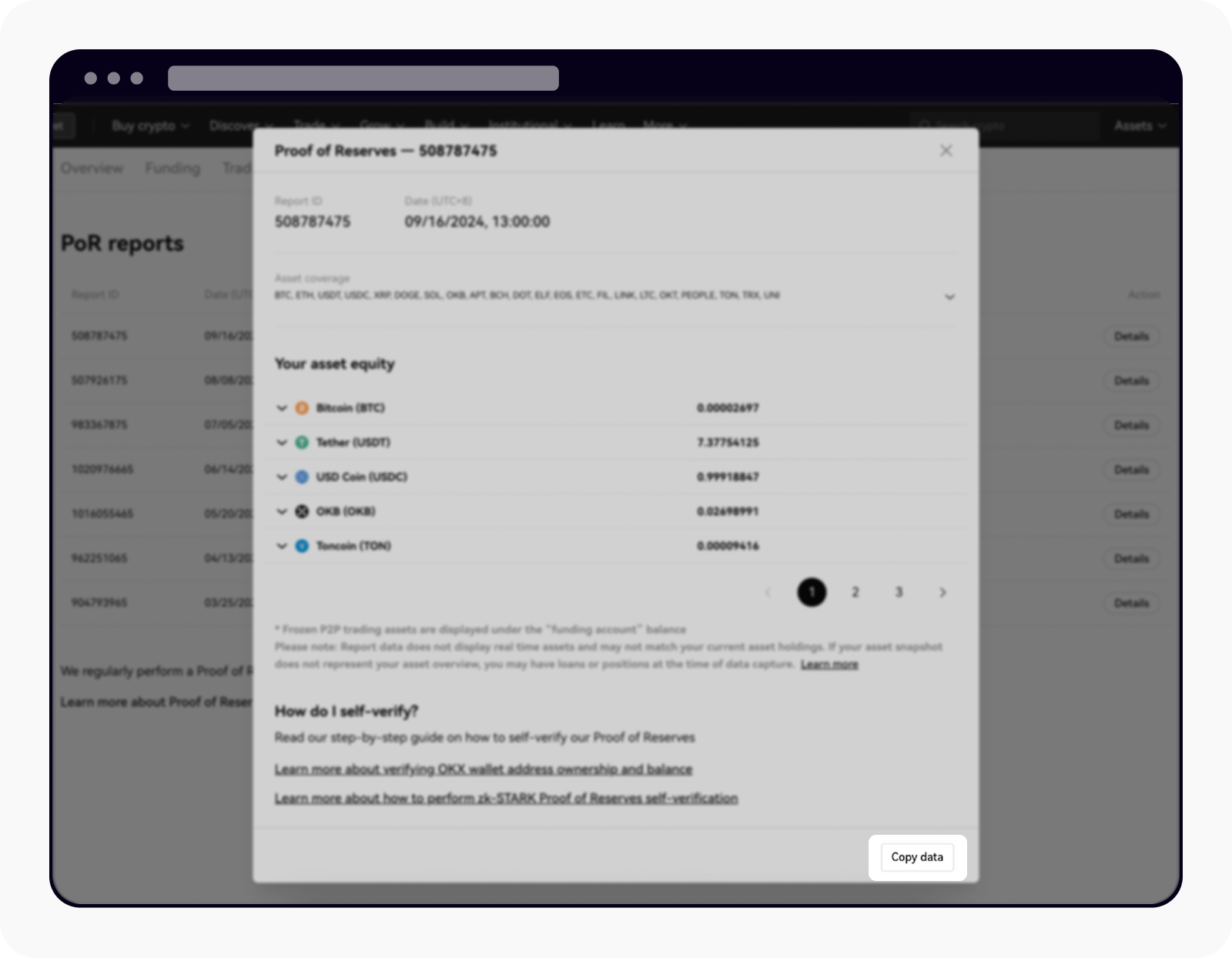
După ce ați selectat Copiere date, deschideți editorul de text (deexemplu folosind Notebook), apoi lipiți și salvați șirul JSON ca fișier. Fișierul trebuie să se încheie cu numele „_inclusion_proof.json.” Șirul JSON conține soldul contului și un instantaneu al căii Merkle. Apoi salvați fișierul într-un dosar nou
Deschide un editor de text (deexemplu, Notebook), apoi lipiți și salvați șirul JSON ca fișier. Numele fișierului trebuie să se încheie cu „_inclusion_proof.json.” Salvați fișierul într-un dosar nou
Șirul JSON conține soldul contului și un instantaneu al căii Merkle.
Textul JSON este afișat mai jos:
{"sum_tree_siblings":["9ffb169fecf075e203edca2af65e4c69fa4331d13ac75ccae4cd5b990c91b675","7149661a789763cb61293ebf5d8bdd5570e79ee203738f87a444c79642b89a79","788aac9e392fa62bc3f79c98c7afd7bb41ee7d5bd496876cd0580080f19e002f","e828a44d345e6799e232aabc57cb2b92986ee1c52b65344d83e79d84b4b571b7","6c0675de9cd6b2be1abd6a98260e7ea776492c4aa9aadf31086f23452cb7c48d","2dfe3aadb5ac00ee0b1110ee8c313afdee85d9f9c62904d6ee79c8f02354d80a","5068ae26192587432892a6de8b54ea25a8aafd1c010ab5e67b55b2c30c6257fa","a1bb026ec9f3d8a1fa1b6f498c40ed8b117a57e1af9816d08d9135ab4fe43a60","119dfcd214191405b7f7f7c7091b89196c0cae818bfcd8252a48f20d9cf3c378","4d9403482ca177c669df34a60bb2afab7a18097012d0b70703c8e59258cdfee6"],"recursive_tree_siblings":[{"right_hashes":["e041eaa366259f873e9e1477aac77362f4b1b460c2d5e1c14907fa9288d66cff","b45a8c503e649ff39543a918996b06fc65f4df9b61d071b22f7342f94862c9be","e00ec1225dfe6b7e950f6b9b8e9d1121bf17eb60c444fd7191b861a2ddddad23","c02c12beb73c03f996508cdce7bef927f0aa8b77ebd899f6a75df83de9d4022e","d36b95f14c5fd5bfaf1347e3177340e2fc9475a77b852321b80527132e7d539c","c0b9770178e70a7bba4ac8aeaadab2bcb2ae7f90d0f678bd463f2c42ff4f4a7b","fab5e7c6f7f8bc6d51f515c5db235cc1ebe987adee8c19c9bc7313e9e266d72c","b3884fb88fc95949c78ca8867cfa9e8a3c4c59fa1a48d8371f7fbfbebda0acfd","0c6da9bdbd40065f92ddaa45297670f2f0bffedb74020c5d5752e70d8b507b77","left_hashes":["1101beee3c6a36a168ceee9d43fcf6cb6de7e5c87ed4d22cd0308c9870d17839","d40a8e9eb4c873996ec515600def480eaa9378ca8481a7bcdf5f77725dbec4ae","63b12566ba8473f502386e92d500664cb63683dca6c26593378dcc9715257b77","166440a8ccbfbc1ce6ec5efaf8bc0b25e1bf692fa972e2729e45ce709d1d35a3","724451ad1d937fc47de5ede930d159dce78093d5e6a1f2e698452f8a29b4de3a","081a88f12d4e23173a1bf5038d4a9413cc92dd421c92261065de06492b5010ec","a76dbb1d4c393539b9546f4460d50ebc7582748d7de63c62c463b793c55bac7c","91e6c21de3f4060e1bd864131a570af42de31bbcd84a5afcbbc8fedcbf806002","fad08eca5bfdc5f37d39eabb44c2216afc6498afcb6b913d72586eaaf132a572","d39b06fe28387ba8045e2b2f95e90613916beef4f79df7961514e6e4cbfd07fa","81d07e300a116a0e4fcb56c39715c5fd5921abe8d10329b07c3f33d417b70ca8","7b72a7e62a45c9958a8a55eec2ba47352f2af701bacba098668589f6a3ce0423","8766bc64c38c2bb4188d89de0e732bca103daaed0c779cba9a8b191e24b51c9c","fa57ae4409e46c605f3cbfd01dfd9ccebc86cbd765cdc067206cb9367832442f"]}, ...... "index":9583119,"account":{"id":"50f5f08cc5036e15a541c64ac4ac6d2d9aa8ddab1ec32ed58b10e6ed3edfad59","debt":["0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"],"equity":["8412384","9386185","45265193","0","0","8751","3824171","2716990","0","313671","28319","0","0","0","41261","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","142353","0","0","0","0","0","4435","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","662","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","993","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","25132","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","305","0","0","0","0","0","0","0","0","6141","0","0","0","0","0","0","0","0","0","0","0","5511","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"]}}
Descărcați instrumentul de verificare cu sursă deschisă OKX: zk-STARKValidator
Salvați instrumentul de verificare cu sursă deschisă OKX, zk-STARKValidator, și fișierul cu șir JSON împreună în noul dosar creat în Pasul 5. În cazul nostru, am plasat instrumentul și fișierul de date în dosarul Descărcări, numit „dovada rezervelor”, așa cum se arată mai jos:

Deschideți zk-STARKValidator; acesta va rula automat fișierul JSON pe care l-ați salvat în dosar
Verificați rezultatul:
Dacă verificarea trece, va fi afișat rezultatul Inclusion constraint validation passed:

Dacă verificarea eșuează, va fi afișat rezultatul Inclusion constraint validation failed:

Cum verific soldul total zk-STARK și constrângerea non-negativă?
Iată cum puteți verifica că activele pe care declarăm că le deținem sunt reale și că niciun utilizator nu deține capital net negativ:
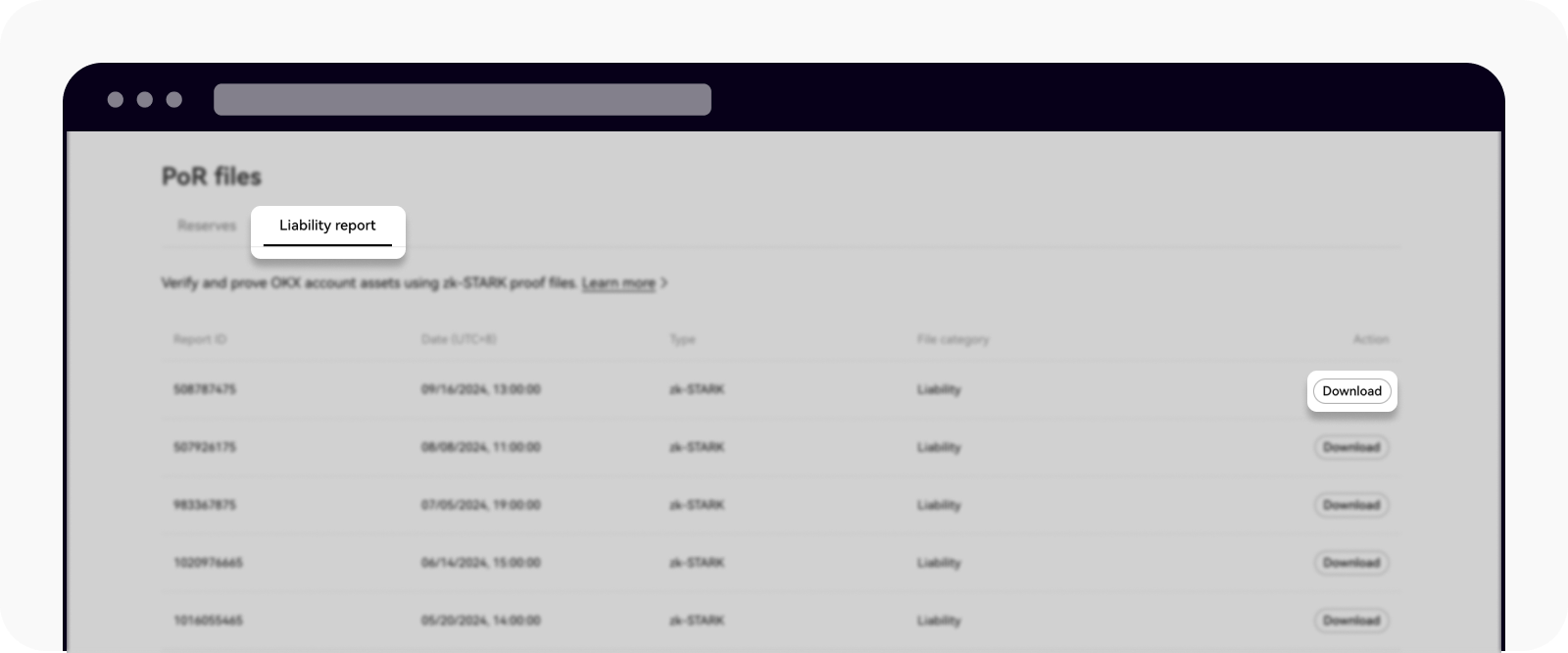
Accesați pagina noastră Dovada rezervelor și selectați Raport de responsabilitate
Descărcați fișierul zk-STARK și salvați-l într-un dosar nou
Dezarhivați fișierul pentru a extrage un fișierul „sum_proof_data.json”

Descărcați instrumentul de verificare cu sursă deschisă OKX: zk-STARKValidator
Salvați instrumentul de verificare cu sursă deschisă OKX, zk-STARKValidator și fișierul „sum_proof_data.json” împreună în noul dosar creat în Pasul 2. În cazul nostru, am plasat instrumentul și fișierul de date în dosarul Descărcări, numit „dovada rezervelor”, așa cum se arată mai jos:

Deschideți zk-STARKValidator; acesta va rula automat fișierul sum proof data pe care l-ați salvat în dosar.
Verificați rezultatul
Dacă verificarea trece, va fi afișat rezultatul Total sum and non-negative constraint validation passed:

Dacă verificarea eșuează, va fi afișat rezultatul Total sum and non-negative constraint validation failed:

Pentru a explora mai multe detalii tehnice, sistemul nostru de dovadă a rezervelor este cu sursă deschisă și disponibil pentru revizuire și utilizare pe github.






