Zero-Knowledge Proof: co jsou zk-STARK a jak fungují? (zk-Stark V2)
Co je Proof-of-Reserve a Zero Knowledge Proof?
Proof-of-Reserve (PoR)
Jedná se o proces, v rámci kterého burzy kryptoměn prokazují, že mají dostatek aktiv na pokrytí všech zůstatků zákazníků. Burzy tak zvyšují svou důvěryhodnost, protože prokazují, že neskrývají žádné závazky. Nejjednodušší způsob, jak to provést, je zveřejnit jak množství aktiv burzy, tak seznam zůstatků uživatelů, aby si to každý mohl ověřit:
Celková držba aktiv uživatelů, které OKX tvrdí, že má, se rovná součtu celkových zůstatků aktiv všech uživatelů.
Celkový zůstatek každého uživatele je větší než nula a jeho aktiva jsou zohledněna tak, že pokrývají jeho závazky a zajišťují, aby měl každý uživatel kladný čistý vlastní kapitál.
Celková hodnota, kterou burza uvádí, se vztahuje na každého jednotlivého uživatele, takže každý uživatel by měl mít možnost ověřit, zda je jeho čistá hodnota zahrnuta do celkové hodnoty
Odhalení těchto zůstatků by však mohlo ohrozit soukromí uživatelů. K vyřešení tohoto problému používáme metodu nazvanou Zero Knowledge Proof (ZKP), která zajišťuje ochranu soukromí uživatelů.
Zero Knowledge Proof (ZKP)
Jedná se o techniku zabezpečení, která umožňuje kryptoměnové burze prokázat, že tvrzení je pravdivé, aniž by odhalila jakékoli další informace.
V našem případě chceme dokázat, že máme dostatek prostředků, aniž bychom sdíleli konkrétní údaje o uživatelích. Většina ZKP spadá do dvou kategorií:
zk-SNARK
zk-STARK
My používáme zk-STARK, protože je bezpečnější a má předpoklad minimálního zabezpečení. V tomto článku vysvětlíme, jak používáme zk-STARK k ochraně soukromí uživatelů při prokazování naší solventnosti. Než budeme pokračovat, bude dobré pochopit některé základní pojmy používané v ZKP, jako jsou obvod, Merkleův strom a závazky.
Pro začátečníky je k dispozici mnoho zdrojů, které vám pomohou do problematiky proniknout. Pokročilé uživatele můžeme odkázat na kurz MOOC a akademickou monografii.
Jak systém zk-STARK funguje?
Vytvoříme Merkleův strom, který má jako listy hashe jednotlivých uživatelských účtů. Každý účet zobrazuje zůstatky různých tokenů (např. BTC, ETH) v USD. S těmito zůstatky nakládáme tak, že je u každého tokenu rozdělujeme na nezáporný kapitál a dluhy. Tímto způsobem pracujeme pouze s kladnými čísly, což usnadňuje provádění výpočtů a zamezuje chybám.
Například:
Pokud má zůstatek tokenu BTC uživatele hodnotu A, jeho vlastní kapitál v BTC je A a dluh v BTC je 0
Pokud má zůstatek tokenu ETH uživatele hodnotu -B, jeho příslušný vlastní kapitál je 0 a dluh je B.
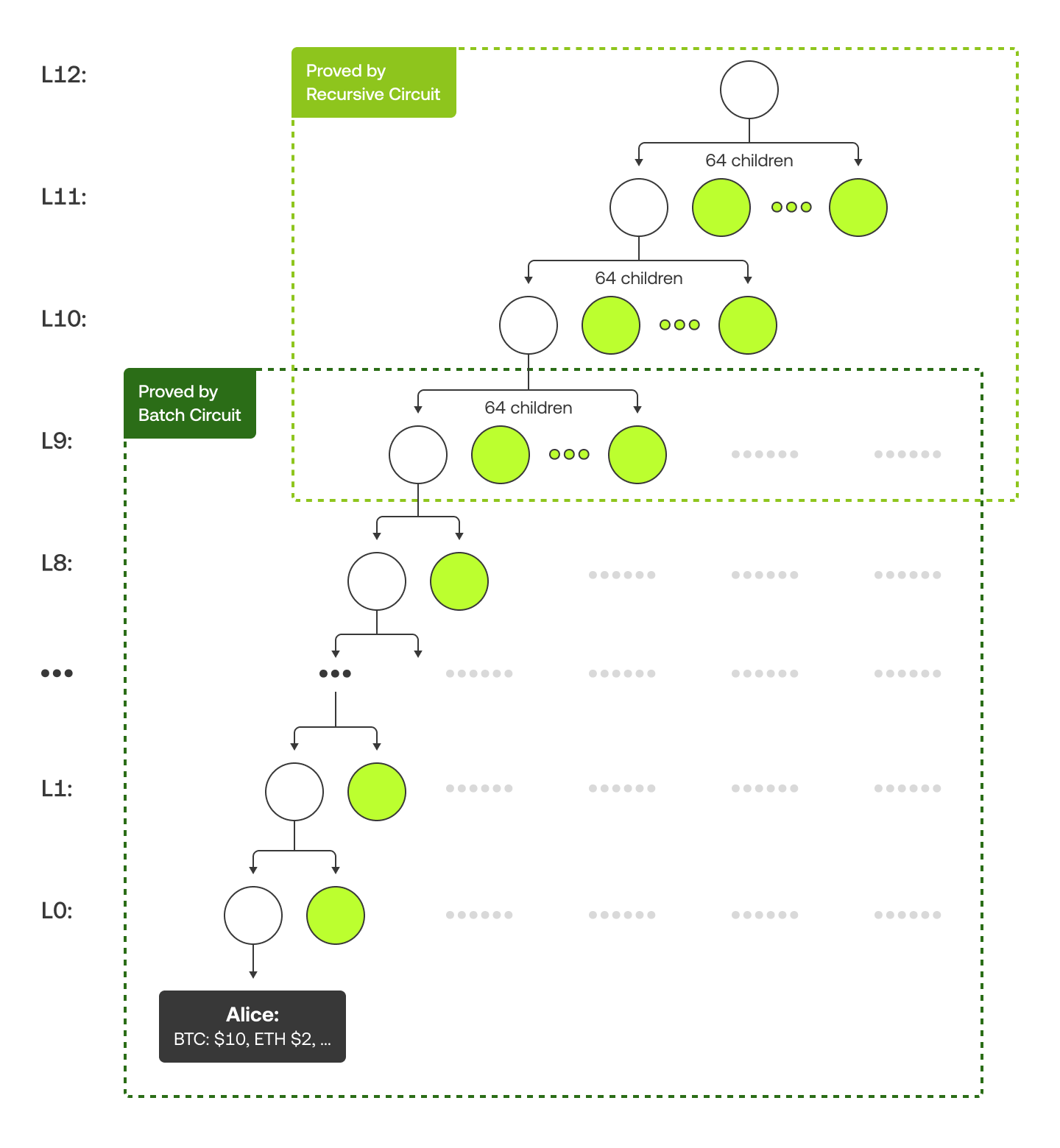
Dále vytvoříme Merkleův strom, u kterého budou listy tvořeny těmito hodnotami účtů. Kořen stromu představuje jedinou hodnotu, která zachycuje všechny zůstatky uživatelů. Každý uživatel může prokázat, že jeho účet je součástí tohoto stromu, pomocí takzvané Merkleovy cesty, která popisuje, jak je jeho účet propojen s kořenem.
Zveřejňujeme také celkový vlastní kapitál a dluh sečtený napříč všemi tokeny a uživateli. Poté vytvoříme Zero Knowledge Proof (ZKP), který prokazuje dvě věci:
Důkaz součtu: součet hodnot vlastního kapitálu a dluhů v Merkleově stromu je správný
Důkaz nezápornosti: celkový kapitál každého uživatele je větší než jeho celkový dluh
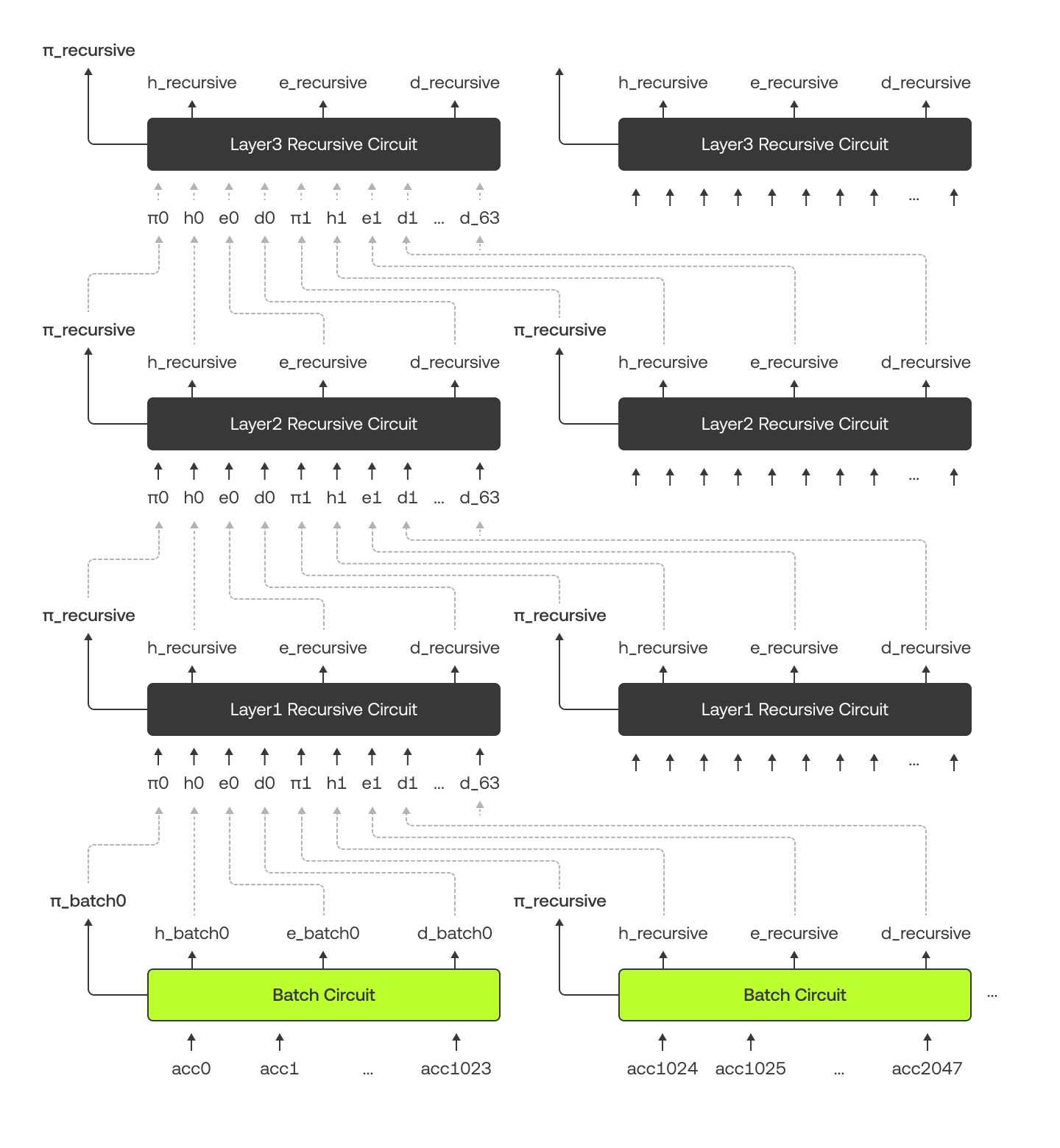
Když se pokusíme ověřit Merkleův strom pro velké množství účtů, bude to najednou příliš obtížné. Abychom tento problém překonali, rozdělíme účty do menších skupin nazývaných dávky. Každá dávka je zpracovávána samostatně pomocí dávkových obvodů, které kontrolují spodní část Merkleova stromu.
Dávkové zpracování nejenže zajišťuje, aby byla tato operace zvládnutelná, ale také nám umožňuje provádět tyto kontroly současně (paralelní zpracování). Jakmile máme výsledky ze všech dávek, použijeme další vrstvu obvodů nazývanou rekurzivní obvody, abychom spojili a ověřili všechny dávky dohromady, dokud neprokážeme celý Merkleův strom.
Co je dávkový obvod?
Dávkový obvod bere jako vstupy 1024 účtů (acc0, acc1,., acc1023) a generuje 3 hlavní výstupy: hash (hbatch), celkovou hodnotu vlastního kapitálu (ebatch), a celkovou hodnotu dluhu (dbatch). Ověřuje následující:
zda je celkový kapitál každého účtu v USD větší než jeho celkový dluh,
zda je ebatch součtem všech hodnot vlastního kapitálu denominovaných v USD napříč těmito účty,
zda je dbatch součtem všech hodnot dluhů denominovaných v USD napříč těmito účty,
zda je hbatch kořen Merkleova stromu vytvořeného pomocí hashů účtů,
zda při sčítání ebatch a dbatch nedochází k přetékání.
Co je rekurzivní obvod?
Rekurzivní obvod bere jako vstupy 64 různých důkazů (π0, …, π63), hashů (h0, …, h63), vlastních kapitálů (e0, …, e63) a dluhů (d0, …, d63) z obvodů nižší vrstvy. Kombinuje tyto vstupy a produkuje 3 výstupy: nový hash (hrecursive), celkový vlastní kapitál (erecursive) a celkový dluh (drecursive). Ověřuje následující:
zda je každý z 64 důkazů platný,
zda je každý důkaz π0, …, π63 z obvodu nižší vrstvy platný,
zda je erecursive součtem e0, …, e63,
zda je drecursive součtem d0, …, d63,
zda je hrecursive hash z řetězení h0, ..., h63, tj.
hrecursive = Hash (h0 || h1 || ... || h63)
zda při sčítání erecursive a drecursive nedochází k přetečení.
Jaký je vztah mezi dávkovými a rekurzivními obvody?
Schéma níže ilustruje, jak jsou propojeny dávkové a rekurzivní obvody a jak si předávají data. Mějte na paměti, že ve schématu obvody pro názornost duplikujeme, ale při skutečné implementaci používáme na každou vrstvu pouze jeden obvod.
Náš Merkleův strom je strukturován trochu jinak. Na spodních 10 úrovních má každý nadřazený uzel 2 podřazené položky, zatímco na vyšších úrovních má každý nadřazený uzel 64 podřazených položek. Je tomu tak proto, že dávkové obvody zpracovávají spodní část a rekurzivní obvody spravují horní část. Schéma níže používá příklad s tokenem „Alice“, aby ukázal Merkleův strom a příslušný Merkleův důkaz (zbarvený zeleně).
Další technické podrobnosti, například to, jak přizpůsobujeme hodnoty účtů velikosti dávky nebo jak vybíráme správný hashovací algoritmus, naleznete na této stránce.
Vylepšení v 2. verzi zk-PoR
Naše 2. verze zk-PoR se oproti předchozí verzi vyznačuje několika vylepšeními:
Větší efektivita: Nyní je 50krát rychlejší než předchozí verze. Na jednom 10jádrovém stroji nyní trvá operace 3 hodiny ve srovnání s 36 hodinami s devíti 64jádrovými stroji u předchozí verze. Toto zrychlení umožnilo použití frameworku Plonky2, který kompiluje obvody kódované v jazyce Rust do efektivního strojového jazyka namísto pomalejších skriptů v Pythonu. Také jsme vylepšili Plonky2, aby některé výpočty prováděl pomocí grafické karty, čímž jsme čas zkrátili o dalších 30 %.
Lepší provádění auditů: 2. verze využívá framework vysoké úrovně, který za nás zpracovává složité kryptografické detaily. Kód je tak přehlednější, čitelnější a méně náchylný k chybám.
Stručný důkaz: Velikost důkazu V2 (cca 500 kB) je pouze 0,05 % V1 (cca 1,2 GB). Díky rekurzivní metodě lze důkazy opakovaně agregovat a zhušťovat do jediného důkazu.
Jak mohu provést vlastní ověření Proof of Reserves (PoR)?
Takto můžete zkontrolovat, zda je váš zůstatek aktiv zahrnuto jako Merkleův list do zk-STARK:
Přihlaste se ke svému účtu OKX, přejděte na možnost Aktiva a vyberte Zprávy PoR
Výběrem možnosti Podrobnosti zobrazíte svá auditní data
Data, která budete pro ruční ověření potřebovat, získáte výběrem možnosti Kopírovat data
Po výběru možnosti Kopírovat data otevřete textový editor (například poznámkový blok), vložte je a řetězec uložte jako soubor JSON. Soubor musí končit názvem „_inclusion_proof.json“. Řetězec JSON obsahuje zůstatek vašeho účtu a snímek Merklovy cesty, soubor pak uložte do nové složky
Otevřete textový editor (například poznámkový blok), vložte data a uložte řetězec JSON jako soubor. Název souboru musí končit „_inclusion_proof.json“. Uložte soubor do nové složky.
Řetězec JSON obsahuje zůstatek vašeho účtu a snímek Merkleovy cesty.
Text JSON je zobrazen níže:
{"sum_tree_siblings":["9ffb169fecf075e203edca2af65e4c69fa4331d13ac75ccae4cd5b990c91b675","7149661a789763cb61293ebf5d8bdd5570e79ee203738f87a444c79642b89a79","788aac9e392fa62bc3f79c98c7afd7bb41ee7d5bd496876cd0580080f19e002f","e828a44d345e6799e232aabc57cb2b92986ee1c52b65344d83e79d84b4b571b7","6c0675de9cd6b2be1abd6a98260e7ea776492c4aa9aadf31086f23452cb7c48d","2dfe3aadb5ac00ee0b1110ee8c313afdee85d9f9c62904d6ee79c8f02354d80a","5068ae26192587432892a6de8b54ea25a8aafd1c010ab5e67b55b2c30c6257fa","a1bb026ec9f3d8a1fa1b6f498c40ed8b117a57e1af9816d08d9135ab4fe43a60","119dfcd214191405b7f7f7c7091b89196c0cae818bfcd8252a48f20d9cf3c378","4d9403482ca177c669df34a60bb2afab7a18097012d0b70703c8e59258cdfee6"],"recursive_tree_siblings":[{"right_hashes":["e041eaa366259f873e9e1477aac77362f4b1b460c2d5e1c14907fa9288d66cff","b45a8c503e649ff39543a918996b06fc65f4df9b61d071b22f7342f94862c9be","e00ec1225dfe6b7e950f6b9b8e9d1121bf17eb60c444fd7191b861a2ddddad23","c02c12beb73c03f996508cdce7bef927f0aa8b77ebd899f6a75df83de9d4022e","d36b95f14c5fd5bfaf1347e3177340e2fc9475a77b852321b80527132e7d539c","c0b9770178e70a7bba4ac8aeaadab2bcb2ae7f90d0f678bd463f2c42ff4f4a7b","fab5e7c6f7f8bc6d51f515c5db235cc1ebe987adee8c19c9bc7313e9e266d72c","b3884fb88fc95949c78ca8867cfa9e8a3c4c59fa1a48d8371f7fbfbebda0acfd","0c6da9bdbd40065f92ddaa45297670f2f0bffedb74020c5d5752e70d8b507b77","left_hashes":["1101beee3c6a36a168ceee9d43fcf6cb6de7e5c87ed4d22cd0308c9870d17839","d40a8e9eb4c873996ec515600def480eaa9378ca8481a7bcdf5f77725dbec4ae","63b12566ba8473f502386e92d500664cb63683dca6c26593378dcc9715257b77","166440a8ccbfbc1ce6ec5efaf8bc0b25e1bf692fa972e2729e45ce709d1d35a3","724451ad1d937fc47de5ede930d159dce78093d5e6a1f2e698452f8a29b4de3a","081a88f12d4e23173a1bf5038d4a9413cc92dd421c92261065de06492b5010ec","a76dbb1d4c393539b9546f4460d50ebc7582748d7de63c62c463b793c55bac7c","91e6c21de3f4060e1bd864131a570af42de31bbcd84a5afcbbc8fedcbf806002","fad08eca5bfdc5f37d39eabb44c2216afc6498afcb6b913d72586eaaf132a572","d39b06fe28387ba8045e2b2f95e90613916beef4f79df7961514e6e4cbfd07fa","81d07e300a116a0e4fcb56c39715c5fd5921abe8d10329b07c3f33d417b70ca8","7b72a7e62a45c9958a8a55eec2ba47352f2af701bacba098668589f6a3ce0423","8766bc64c38c2bb4188d89de0e732bca103daaed0c779cba9a8b191e24b51c9c","fa57ae4409e46c605f3cbfd01dfd9ccebc86cbd765cdc067206cb9367832442f"]}, . . "index":9583119,"account":{"id":"50f5f08cc5036e15a541c64ac4ac6d2d9aa8ddab1ec32ed58b10e6ed3edfad59","debt":["0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"],"equity":["8412384","9386185","45265193","0","0","8751","3824171","2716990","0","313671","28319","0","0","0","41261","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","142353","0","0","0","0","0","4435","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","662","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","993","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","25132","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","305","0","0","0","0","0","0","0","0","6141","0","0","0","0","0","0","0","0","0","0","0","5511","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"]}}
Stáhněte si opensourcový ověřovací nástroj OKX: zk-STARKValidator
Uložte opensourcový ověřovací nástroj OKX zk-STARKValidator a soubor JSON společně do nové složky vytvořené v 5. kroku. V našem případě uložíme nástroj i datový soubor do složky Stažené soubory a pojmenujeme je „proof-of-reserves“, jak je uvedeno níže:

Otevřete zk-STARKValidator, který automaticky spustí soubor JSON, který jste uložili do složky.
Zkontrolujte výsledek:
Pokud ověření proběhne úspěšně, zobrazí se výsledek Ověření omezení zahrnutí bylo úspěšné:

Pokud ověření proběhne neúspěšně, zobrazí se výsledek Ověření omezení zahrnutí se nezdařilo:
Jak ověřím celkový zůstatek zk-STARK a omezení nezápornosti?
Takto můžete ověřit, že informace o aktivech, o kterých tvrdíme, že je máme v držení, jsou pravdivé a že žádný uživatel nemá záporný čistý kapitál:
Přejděte na naši stránku Proof of Reserve a vyberte možnost Zpráva o závazcích
Stáhněte si soubor zk-STARK a uložte ho do nové složky
Rozbalte soubor a extrahujte soubor „sum_proof_data.json“

Stáhněte si opensourcový ověřovací nástroj OKX: zk-STARKValidator
Uložte opensourcový ověřovací nástroj OKX zk-STARKValidator a soubor „sum_proof_data.json“ společně do nové složky vytvořené v 2. kroku. V našem případě uložíme nástroj i datový soubor do složky Stažené soubory a pojmenujeme je „proof-of-reserves“, jak je uvedeno níže:

Otevřete zk-STARKValidator, který automaticky spustí soubor dat důkazu součtu, který jste uložili do složky
Zkontrolujte výsledek:
Pokud ověření proběhne úspěšně, zobrazí se výsledek Ověření celkového součtu a omezení nezápornosti bylo úspěšné:

Pokud ověření proběhne neúspěšně, zobrazí se výsledek Ověření celkového součtu a omezení nezápornosti bylo neúspěšné:

Pokud chcete prozkoumat další technické podrobnosti, je náš systém Proof of Reserves je open-source a dostupný ke kontrole a použití v systému github.






